This quiz section contains a CCNA practice quiz on router basics. You can test your skills on the basics functionalities of a router in networking. The following quiz section contains multiple-choice questions, drag and drops as well as “refer to the exhibit” questions as per the CCNA 200-301 Exam pattern.
This quiz section contains a CCNA practice quiz on router basics. You can test your skills on the basics functionalities of a router in networking. The following quiz section contains multiple-choice questions, drag and drops as well as “refer to the exhibit” questions as per the CCNA 200-301 Exam pattern.
The CCNA practice quiz is very helpful for the preparation for CCNA 200-301 certification exam.
Each question is provided with the correct answer and an explanation for the correct answer. Click on the button named “Answer” just below the question to view the answer and the explanation. You can hide the answer and the explanation by re-clicking the “Answer” button.
CCNA Practice Quiz- Router Basics
|
1. Which of the following are the major components of the router? Choose any three.
Answer: A, B and C Explanation: The correct options are A, B and C.
|
|
2. Which of the following statements is not true about the functions of RAM in a router?
Answer: Option C Explanation: The configuration register is stored in NVRAM. RAM only stores running configuration and routing tables. RAM doesn’t retain data when turned off.
|
|
3. Which of the following statements is true about the function of NVRAM in a router?
Answer: Option D Explanation: All of the above options are correct.
|
|
4. Which of the following is true about the function of the router? Choose any three
Answer: Options A, B and C Explanation: The router does have multiple broadcast domain and multiple collision domains.
|
|
5. You are asked to configure the IP address to the serial 0/0 interface of the router. In which configuration mode, you need to issue the command to configure the IP address to the serial interface?
Answer: Option C Explanation: The correct sequence of command to configure ip address to serial interface s0/0 is-
Router(config)#interface s0/0
Router(config-if)#ip address <IP address> <Subnet mask>
Router(config-if)#no shutdown
|
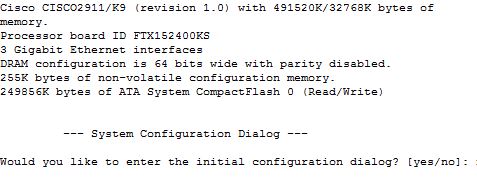
6. You purchased the new router. How the router boots up when it does not find any startup configuration?
|
7. What is the default value of the configuration register in the Cisco router?
Answer: Option A Explanation: The correct option is A.
The default values of the configuration register in the Cisco router is 0x2102.
The configuration register is a 16-bit hexadecimal number that decides the different booting options for the router. This value is stored in NVRAM.
|
|
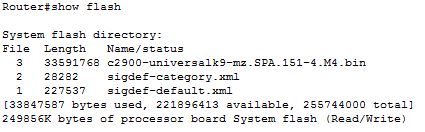
8. Which of the following CLI command will display the name of all the IOS image files available in flash memory?
|
9. What is ROMMON mode in the Cisco router?
Answer: Option C Explanation: The correct option is C.
ROMmon is a small bootstrap program that is stored in ROM to initialize the booting process. When the router does not find the valid IOS in flash, then it jumps into ROMmon mode for diagnostics.
|
|
10.You want to execute the “enable” command to switch from user exec mode to privileged exec mode. What is the current router prompt is displayed on the screen at this point?
Answer: Option B Explanation: The correct option is B.
|
|
11. Which of the following command is not the correct way to execute the CLI command to copy content from RAM to NVRAM?
Answer: Option C Explanation: “copy RAM NVRAM” is not the correct way to copy content from RAM to NVRAM.
|
|
12. You want to upgrade the existing IOS image with a new image from the TFTP server. What command will you execute to download the new IOS image to your router?
Answer: Option A Explanation: The correct option is A.
|
13. Which of the following shows the problem in layer 1, when you issue the “show IP interface” command?
Answer: Option C Explanation: The correct option is C.
|
14. The command “show cdp neighbors” provide the information regarding _____________ layers.
Answer: Option D Explanation: The correct option is D.
|
|
15. You want to set some informative messages for administrators, when the router boots up, what command will you issue?
Answer: Option A Explanation: The correct option is A.
|
|
16. The following command on a Cisco router will display the configurable parameters and statistics of all communication interfaces.
Answer: Option B Explanation: The correct option is B.
|
17. The following command is issued to configure all the default VTY ports on a router.
Answer: Option A Explanation: The correct option is A.
|
|
18. By default, Cisco router supports _________ simultaneous Telnet session.
Answer: Option E Explanation: The correct option is E.
|
|
19. When you erase all the contents of NVRAM and reboot the router, in what mode does it reboot again?
Answer: Option B Explanation: The correct option is B.
|
|
20. Which of the following command is used to issue the secret password ***** to go from user mode to privileged mode?
Answer: Option A Explanation: The correct option is A.
|
| ← Prev | Next → |